Comment résoudre des équations à deux inconnues ?

Si en quatrième, vous avez appris à résoudre une équation à une inconnue, en troisième, vous devrez réussir à résoudre des équations à deux inconnues !
Pas de panique : avec la bonne méthode et un peu d’entraînement, vous devriez y arriver sans aucun problème et réussir votre épreuve de mathématiques au brevet des collèges.
Dans cet article, on vous donne des exemples, deux méthodes de résolution et des exercices pour vous entraîner (faites-les bien avant de regarder la solution !).
Qu’est-ce qu’une équation à 2 inconnues ?
Comment faire une équation à deux inconnues ?
Une équation linéaire à deux inconnues est une égalité dans laquelle figure deux nombres inconnus désignés en général par deux lettres différentes (bien souvent x et y).
Contrairement au résultat d’une équation à une inconnue, les résultats d’une équation à deux inconnues se présentent sous la forme d’un couple de valeurs (x, y) et non d’une seule valeur. Le couple de valeurs est une solution de l’équation.
Exemple et résolution d’une équation linéaire à deux inconnues
2x + y = 4 est une équation linéaire à deux inconnues : x et y.
Pour résoudre une équation linéaire à deux inconnues, il faut trouver tous les couples de solution.
Par exemple :
(2, 3) n’est pas un couple de solutions valables :
2 x 2 + 3 = 7 ≠ 4
En revanche, (-2, 8) et (1, 2) sont des couples de solutions :
2 x (-2) + 8 = 4
2 x 1 + 2 = 4
Ici, on y va par tâtonnement. Vous commencerez de cette manière quand il faudra parler des équations à deux inconnues. Mais rapidement, vous passerez à la résolution de système de deux équations à deux inconnues.
Qu’est-ce qu’un système de deux équations linéaires à deux inconnues ?
Un système de deux équations linéaires à deux inconnues est constitué de deux équations ayant les mêmes inconnues.
Résoudre un système, c’est alors trouver un couple de valeurs qui sera la solution des deux équations.
Tout au long de la résolution d’un système, il faut veiller à garder deux équations.
Comment résoudre un système de deux équations à deux inconnues par substitution ?
Apprenons d’abord à résoudre un système de deux équations à deux inconnues à l’aide de la méthode de la substitution.
Soit le système suivant :
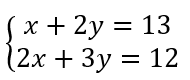
Il faut d’abord isoler l’une des deux inconnues dans l’une des deux équations. Ici, il est plus simple d’isoler x dans la première équation parce qu’il n’a pas de coefficient.
x = 13 - 2y
26 - 4y + 3y = 12
Commençons par la deuxième équation :
26 - 4y + 3y = 12
D'abord, simplifions l'équation en combinant les termes similaires (les termes en y) :
26 - y = 12
Ensuite, isolons y en soustrayant 26 des deux côtés :
- y = 12 - 26
- y = -14
Maintenant, divisons chaque côté par -1 pour obtenir y :
y = -14 / -1 y = 14
Maintenant que nous avons la valeur de y, utilisons-la dans la première équation pour trouver x :
x = 13 - 2y x = 13 - 2 x 14
Calculons : x = 13 - 28 x = -15
Donc, les solutions du système d'équations sont x = -15 et y = 14.
Exercice : comment on fait la méthode de substitution ?
Soit le système suivant :
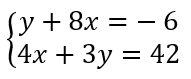
Résoudre le système avec la méthode de substitution.
Réponse :
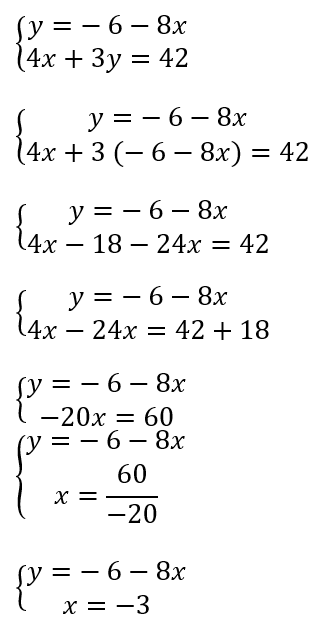
Il ne reste plus qu’à remplacer x par -3 dans la première équation.
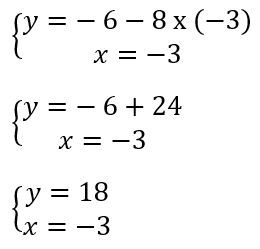
L’unique solution de ce système est le couple (-3, 18) – le x est toujours le premier résultat qu’on donne.
Comment résoudre un système de deux équations à deux inconnues par combinaison linéaire ?
Apprenons maintenant à résoudre un système de deux équations à deux inconnues par combinaison linéaire.
Soit le système suivant :
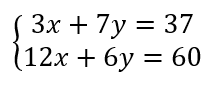
On constate que 12 est un multiple de 3 donc on commence par multiplier la première équation par 4 pour obtenir le même coefficient pour l’inconnue x dans les deux équations. Il ne faut pas oublier de multiplier les deux membres de l’équation par la même valeur.
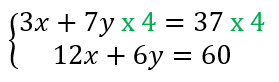
Continuons la résolution à partir du système suivant :
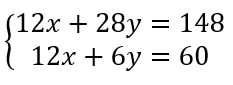
Comme nous avons le même coefficient pour l’inconnue x, on peut soustraire la deuxième équation à la première. Pour ça, il faut soustraire le membre de gauche de la deuxième équation au membre de gauche de la première équation et le membre de droite de la deuxième équation avec le membre de droite de la première.
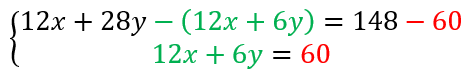
Vous devez ensuite effectuer les calculs en faisant bien attention aux signes.
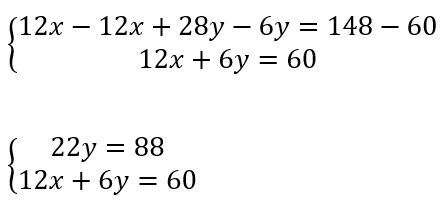
La première équation du système se retrouve avec une seule inconnue. Pour continuer la résolution, il faut diviser cette équation par le coefficient de l’inconnue y. Attention à bien diviser les deux membres de l’équation par la même valeur.
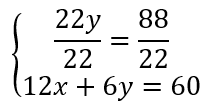
Nous obtenons :
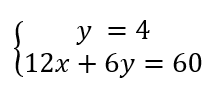
Pour continuer la résolution du système, il suffit de remplacer y dans la deuxième équation par sa valeur dans la première. Ainsi, la deuxième équation devient elle aussi une équation à une inconnue.

Nous avons trouvé un couple de valeurs, solution du système d’équation à deux inconnues : (3, 4), le x étant toujours avant le y.
Vous pouvez vérifier que vous n’avez pas fait d’erreur en reprenant le système du début et en remplaçant x et y par les valeurs trouvées.
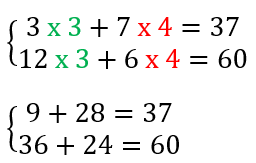
Les additions sont bien justes, on ne s’est donc pas trompés dans la résolution du système d’équations à deux inconnues.
Exercice : à vous de résoudre un système avec la méthode de combinaison
Soit le système suivant :
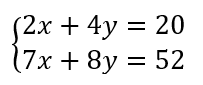
Trouvez le couple de valeurs x et y.
Réponse :
Il faut commencer par transformer les équations pour avoir le même coefficient devant x ou y. On voit que 8 est un multiple de 4. Il faut donc multiplier la première équation par 2.
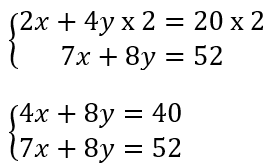
On soustrait ensuite la deuxième équation à la première en faisant attention aux signes :
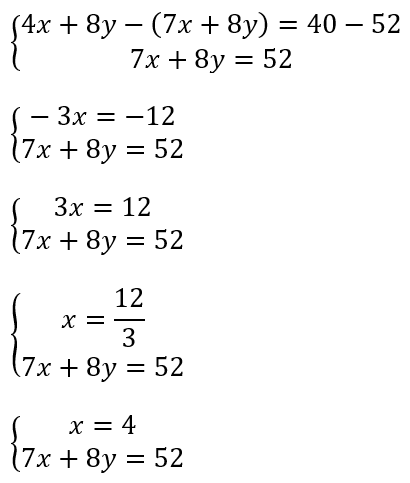
On remplace ensuite le x dans la deuxième équation par la valeur trouvée dans la première équation.
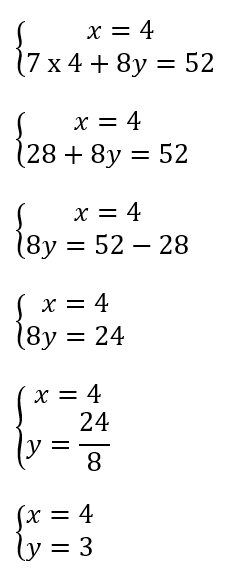
Et on obtient le couple de valeurs (4, 3), solution du système d’équation à deux inconnues.
Dans les faits, vous pourrez choisir de résoudre un système avec la méthode que vous préférez, sauf s’il est clairement précisé dans l’exercice que vous devez utiliser la méthode de substitution ou la méthode de combinaison.
Et si ce n’est pas clair pour vous, nous vous recommandons de faire appel à un professeur particulier de mathématiques pour vous aider à mieux comprendre. Vous trouverez forcément un prof près de chez vous (ou à distance si vous préférez) en passant par le site Superprof !

