Tout savoir sur le théorème de Thalès
Avec le théorème de Pythagore, le théorème de Thalès fait partie des fondamentaux de la géométrie à maîtriser pour un élève de troisième. Il y a de grandes chances pour que des exercices sur ce théorème mathématique soient posés au brevet des collèges !
Sa maîtrise est aussi requise pour passer le Tage Mage de certaines écoles de commerce et le test Score IAE Message.
Alors mieux vaut comprendre de quoi il s’agit, à quoi il sert et comment l’utiliser pour réussir les exercices haut la main. On vous explique tout dans cet article !
Définition du théorème de Thalès en maths
Le théorème de Thalès est une théorie mathématique énoncée par le philosophe grec et savant du nom de Thalès de Milet, 500 ans avant Jésus-Christ.
La première fois qu’il a utilisé ce théorème, c’était pour déterminer les propriétés de la pyramide de Khéops en Égypte. La classe, non ?
Le théorème de Thalès affirme que dans un triangle, une droite parallèle à l’un des côtés du triangle définit un deuxième triangle aux angles proportionnels à l’aide des deux autres côtés.
A quoi sert le théorème de Thalès en cours ?
C’est bien beau de connaître la définition du théorème mais c’est encore mieux de savoir à quoi il sert.
Vous vous en servirez dans les exercices de mathématiques pour calculer une longueur au sein de certaines figures géométriques.
La réciproque sert quant à elle à démontrer que des droites sont parallèles ou au contraire qu’elles ne le sont pas.
De quoi a-t-on besoin pour utiliser le théorème de Thalès ?
Quand appliquer le théorème de thalès ?
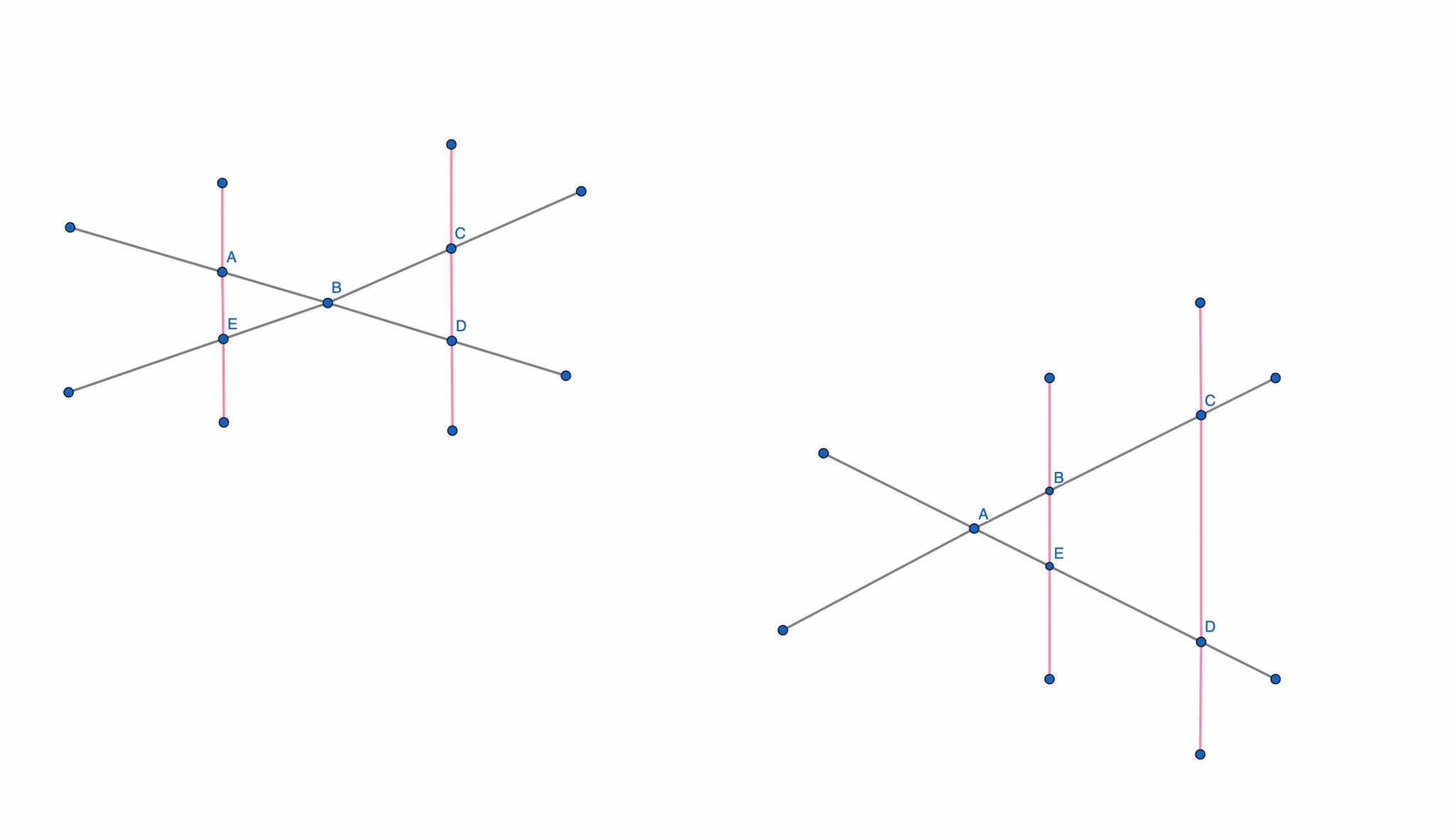
Pour pouvoir utiliser le théorème, vous devez être en présence d’une figure géométrique correspondant à deux droites parallèles coupées par deux droites sécantes.
Le théorème pourra s’appliquer seulement dans deux cas (voir le schéma ci-dessous) :
Deux droites sécantes et deux droites parallèles viennent former deux triangles distincts, reliés entre eux par un sommet
Deux droites sécantes et deux droites parallèles viennent former deux triangles emboîtés avec un sommet commun
Pour rappel :
Deux droites sont parallèles si elles n’ont aucun point en commun. Elles sont distinctes et ne se croiseront jamais.
Deux droites sont sécantes si elles se croisent en un point, nommé point d’intersection.
Vous devez également connaître au moins trois longueurs dans ce type de figure pour pouvoir vous servir du théorème de Thalès.
Quelle est la formule pour le théorème de thalès ?
Exemple du théorème de Thalès
Dans un exercice de mathématiques, vous serez en présence d’une figure géométrique et d’un énoncé vous demandant de calculer une longueur au sein de la figure.
Par exemple :
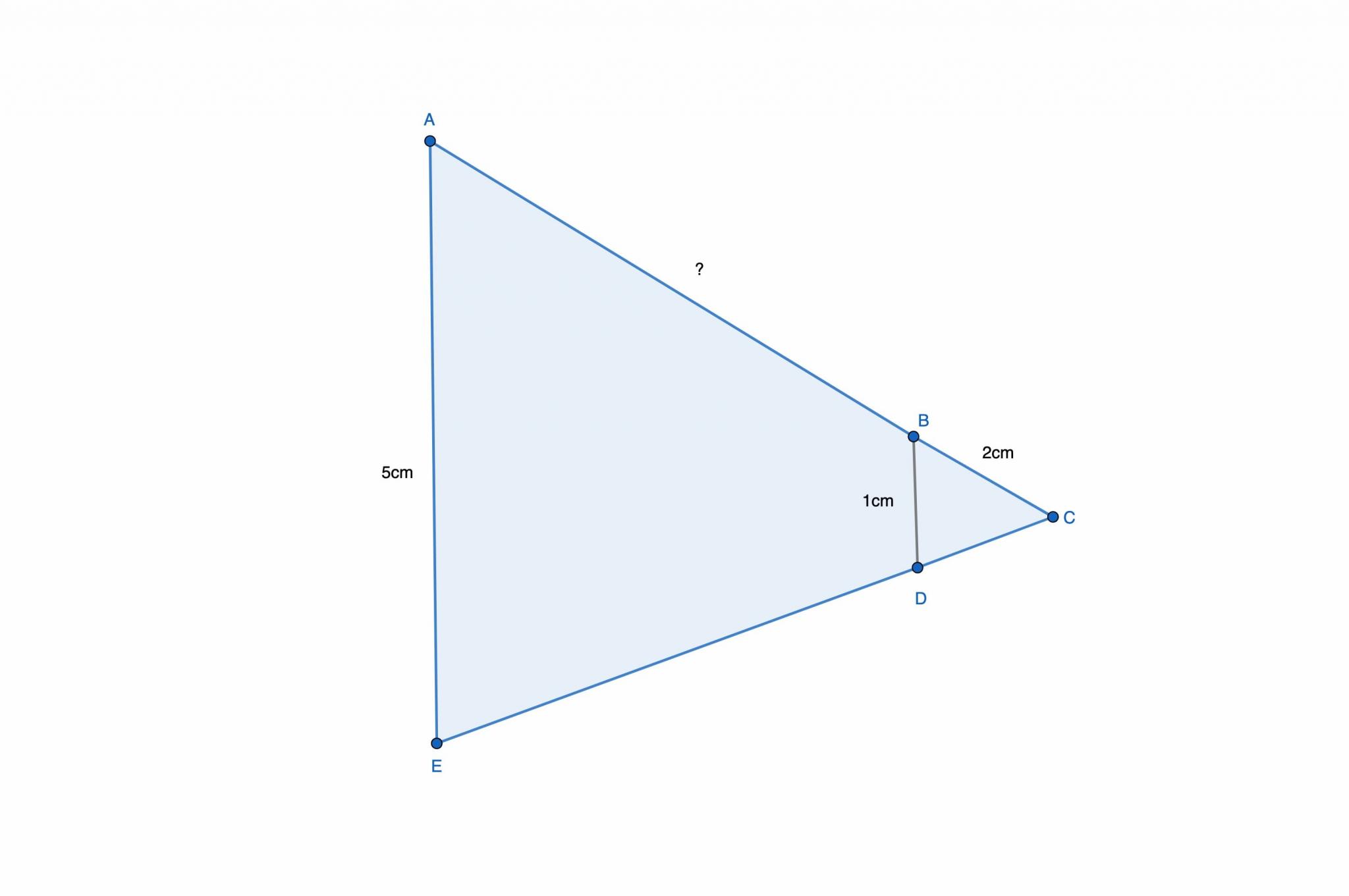
Énoncé : Calculez la longueur de AC et déduisez celle de AB.
Soit un triangle ACE et deux points B et D, B sur la droite (AC) et D sur la droite (EC), de sorte que la droite (BD) soit parallèle à la droite (AE) comme indiqué sur l’illustration ci-dessus.
Selon le théorème de Thalès :
CB/CA = CD/CE = BD/AE
2/CA = CD/CE = 1/5
2/CA = 1/5
CA = (2 x 5) / 1
CA = 10 / 1
CA = 10
AB = CA – CB
AB = 10 – 2
AB = 8
Ainsi, CA mesure 10 cm et AB mesure 8 cm.
Place à l’exercice sur le théorème de Thalès : appliquer la formule
Enoncé du problème :
Soit la figure ci-dessous :
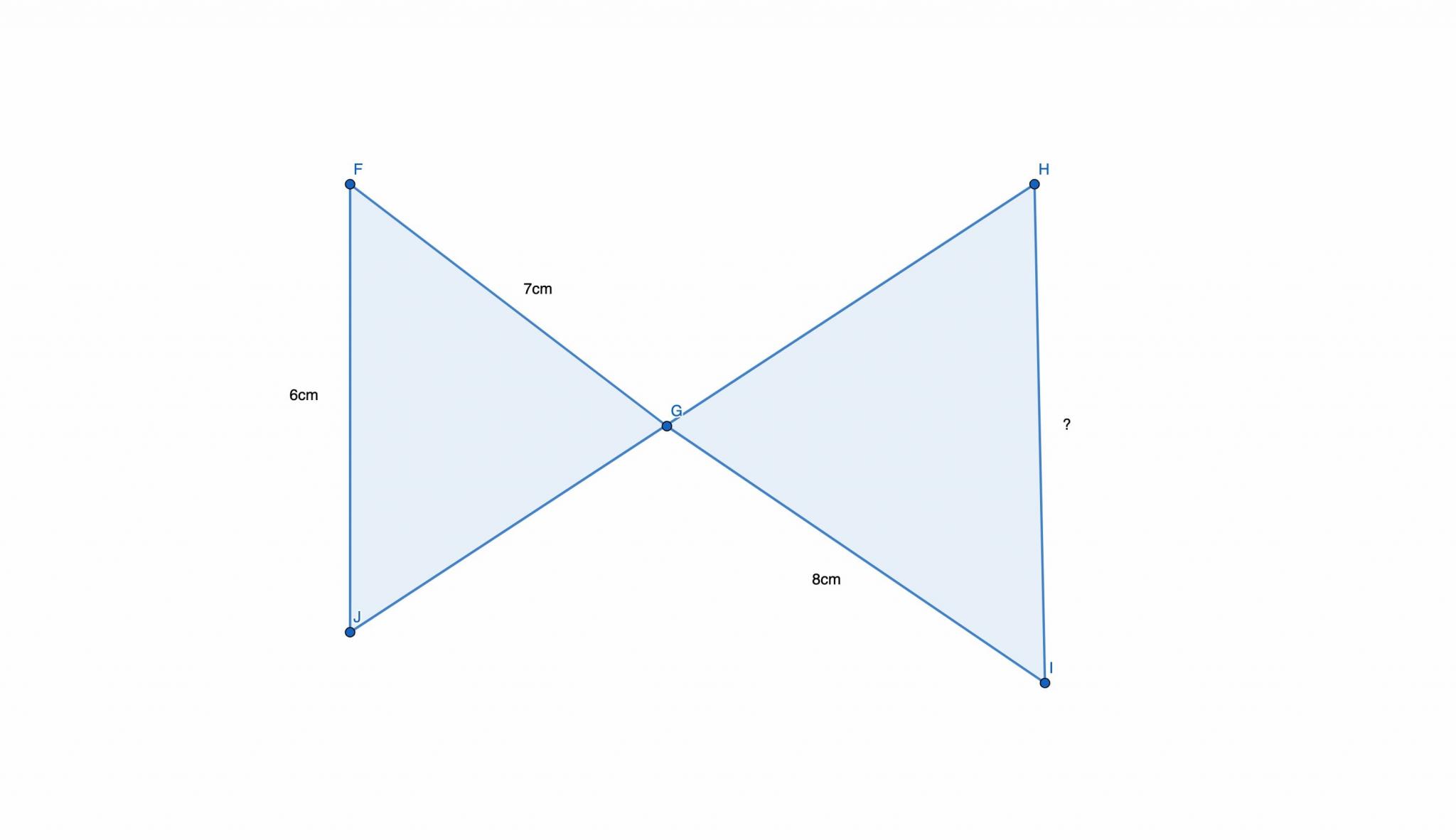
En utilisant le théorème de Thalès, calculez la longueur du segment HI en centimètres à 0,1 près.
Réponse :
Soit deux triangles GFJ et GHI. On sait que les droites (FJ) et (HI) sont parallèles.
Selon le théorème de Thalès :
GJ/GH = GF/GI = FJ/HI
On remplace :
GJ/GH = 7/8 = 6/HI
7/8 = 6/HI
HI = (6 x 8) / 7
HI = 48 / 7
HI = 6,9
Ainsi HI mesure environ 6,9 cm.
Comment démontrer que deux droites sont parallèles ? La réciproque de Thalès
Pour utiliser la réciproque du théorème de Thalès, il faudra connaître quatre mesures. La réciproque sert à prouver que deux droites sont parallèles ou au contraire à le réfuter.
Soit la figure ci-dessous :
On vous demande de prouver que (BE) est parallèle à (CD). Pour cela, il va falloir calculer AE/AD dans un premier temps et calculer ensuite BE/CD.
AE/AD = 3/(3+6) = 3/9 = 1/3
BE/CD = 2/6 = 1/3
Ainsi AE/AD = BE/CD donc d’après la réciproque du théorème de Thalès, les deux droites sont parallèles.
Si les résultats obtenus après calcul sont différents, cela signifie que les deux droites ne sont pas parallèles.
Place à l’exercice sur la réciproque du théorème de Thalès
Soit la figure ci-dessous :
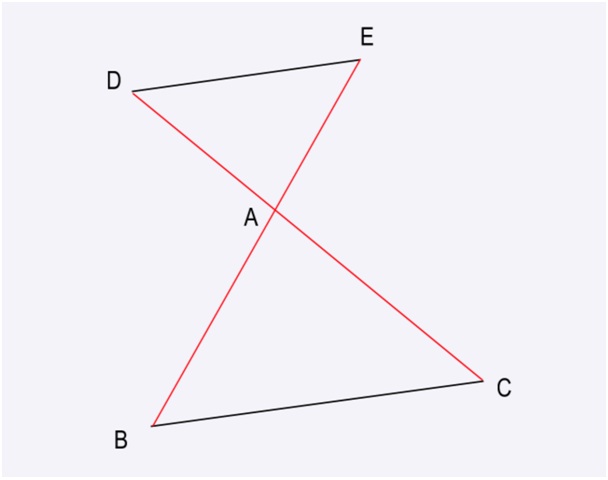
Nous connaissons les mesures suivantes :
DA = 4 cm, AC = 10 cm, DE = 3 cm, BC = 7 cm
Les segments DE et BC sont-ils parallèles ?
Et voici la réponse avec la démonstration appropriée :
DA/AC = 4/10 = 2/5
DE/BC = 3/7
Pour être sûr, vous pouvez faire un produit en croix :
3 x 10 = 30
7 x 4 = 28
Les résultats ne sont pas égaux donc selon la réciproque du théorème de Thalès, les segments DE et BC ne sont pas parallèles.
Comme le théorème de Pythagore, le théorème de Thalès est une notion fondamentale en mathématiques au collège.
Si malgré vos efforts, vous ne parvenez pas à travailler seul les exercices de mathématiques sur le théorème de Thalès, le plus simple est de faire appel à un professeur particulier. Il vous accompagnera, trouvera l’explication qui fera mouche pour vous et vous permettra de préparer votre brevet des collèges en maths pour avoir une bonne note !
Vous pouvez trouver un professeur de maths près de chez vous ou en visio en passant par le site Superprof. Plus de 180 000 profs de mathématiques n’attendent que vous partout en France !
Théorème de Thalès en exercice : le quiz de révision
Après avoir lu cet article, vous êtes surement incollable sur le théorème de Thalès ! Prêt à mettre vos connaissances à l'épreuve avec notre quiz de révision ? ⬇️
